
The preparatory reading for this section is Chapter 4 [Karris, 2012] which presents examples of the applications of the Laplace transform for electrical solving circuit problems. Much of the same material is covered in Section 3.7 D of [Hsu, 2020] .

We look at applications of the Laplace Transform for circuit analysis. In particular we will consider
% initialize MATLAB clearvars format compact syms t L R C i_R(t) v_R(t) i_L(t) v_L(t) v_C(t) i_C(t)
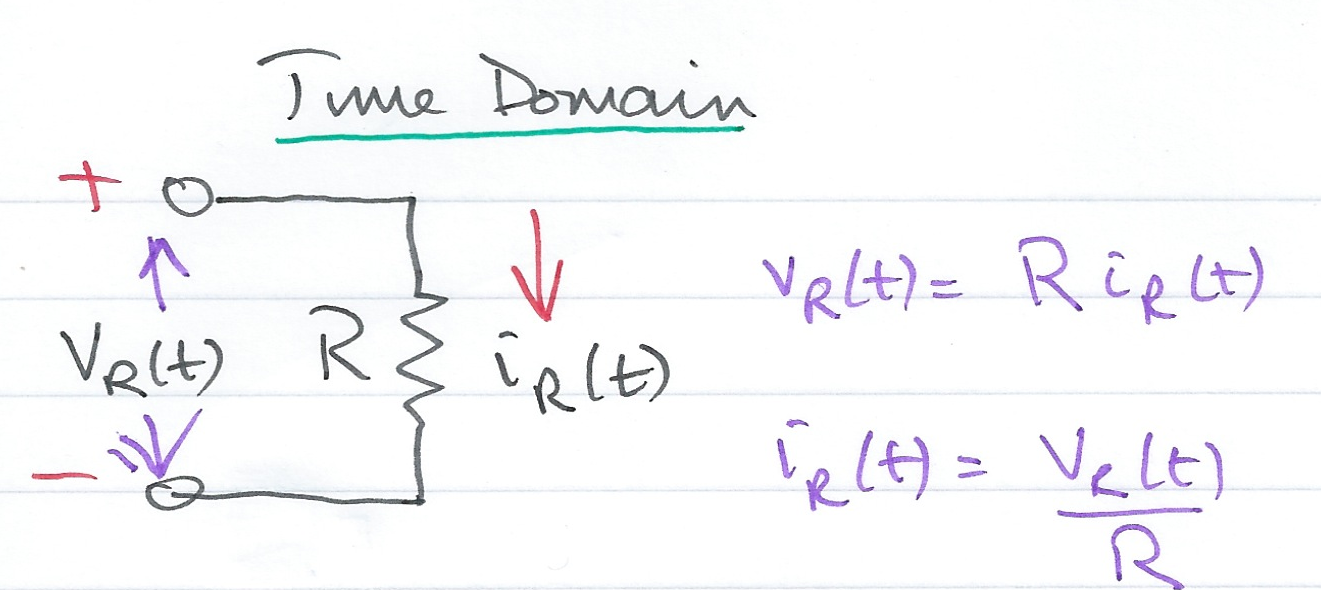
In Fig. 51 the voltage across the resistor \(v_R(t)\) is proportional to the current flowing through the resistor \(i_R(t)\)
(18)# \[v_R(t) = R i_R(t)\]eqvrt = v_R(t) == R * i_R(t)
eqvrt =
v_R(t) == R*i_R(t)
The current flowing through the resistor is inversely proportional to the voltage across the resistor. This is easily confirmed by rewriting (18) to isolate \(i_R(t)\)
eqirt = isolate(eqvrt,i_R(t))
eqirt =
i_R(t) == v_R(t)/R
Rewritten nicely as
(19)# \[i_R(t) = \frac\]From these results, which of the following equations represent the Laplace transform of the current flowing through, and the voltage across, the resistor \(R\) ?
\[V_R(s) = RI_R(s)\] \[I_R(s) + \frac\] \[V_R(s) = \frac\] \[I_R(s) = RV_R(s)\]-> Open poll
We take the Laplace transforms of (18) and (19) to obtain
(20)# \[V_R(s) = R I_R(s)\] (21)# \[I_R(s) = \frac\]which we illustrate in Fig. 52 .
The current and voltage are transformed but the resitance is unchanged by the transformation.

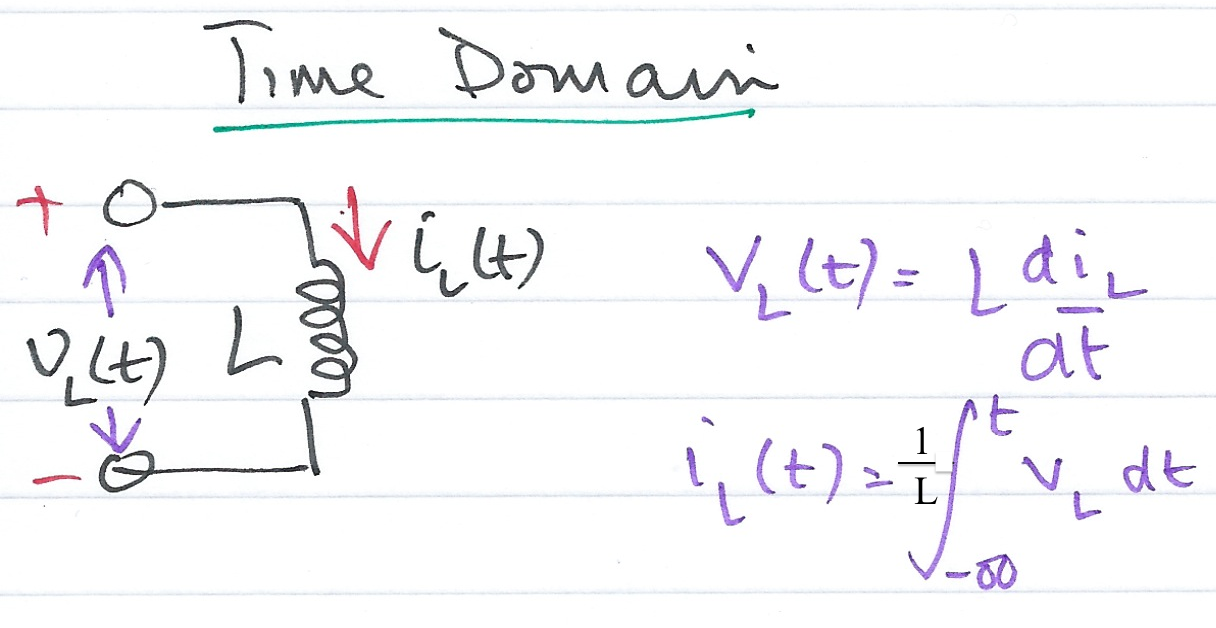
The voltage across the inductor \(i_L(t)\) is proportional to the rate of change of the current \(i_L(t)\) flowing through the inductor
(22)# \[v_L(t) = L \frac i_L(t) \]eqvlt = v_L(t) == L*diff(i_L(t))
eqvlt =
v_L(t) == L*diff(i_L(t), t)
The current flowing through the inductor is inversely proportional to the integral of the voltage across the inductor which is easily confirmed by taking the integral of both sides of (22) and rewriting the equation to isolate \(i_L(t)\)
int(lhs(eqvlt)) == int(rhs(eqvlt)); eqilt = isolate(ans,i_L(t))
eqilt =
i_L(t) == int(v_L(t), t)/L
Rewritten nicely as
(23)# \[i_L(t) = \frac\int_<-\infty>^ v_L(t)\, dt\]From these results, which of the following equations represent the Laplace transform of the current flowing through, and the voltage across, the inductor \(L\) ?
\[I_L(s)=sLV_L(s) - v_L(0^-)\] \[I_L(s)=\frac + \frac\] \[V_L(s) = sLI_L(s) - i_L(0^-)\] \[V_L(s)=\frac + \frac\]-> Open poll

We take the Laplace transforms of (22) and (23) to obtain
(24)# \[V_L(s) = s L I_L(s) - i_L(0^-)\] (25)# \[I_L(s) = \frac + \frac\]The current and voltage are transformed but so is the inductance. The complex frequency representation has used the derivative property for the voltage across the inductor and the integration properties for the current through the inductor. The use of the dervative and integration transforms has introduced a term that depends on the initial current flowing through the inductor. Therefore, the initial current would need to be considered in computing the actual voltage and current in the complex frequency domain.
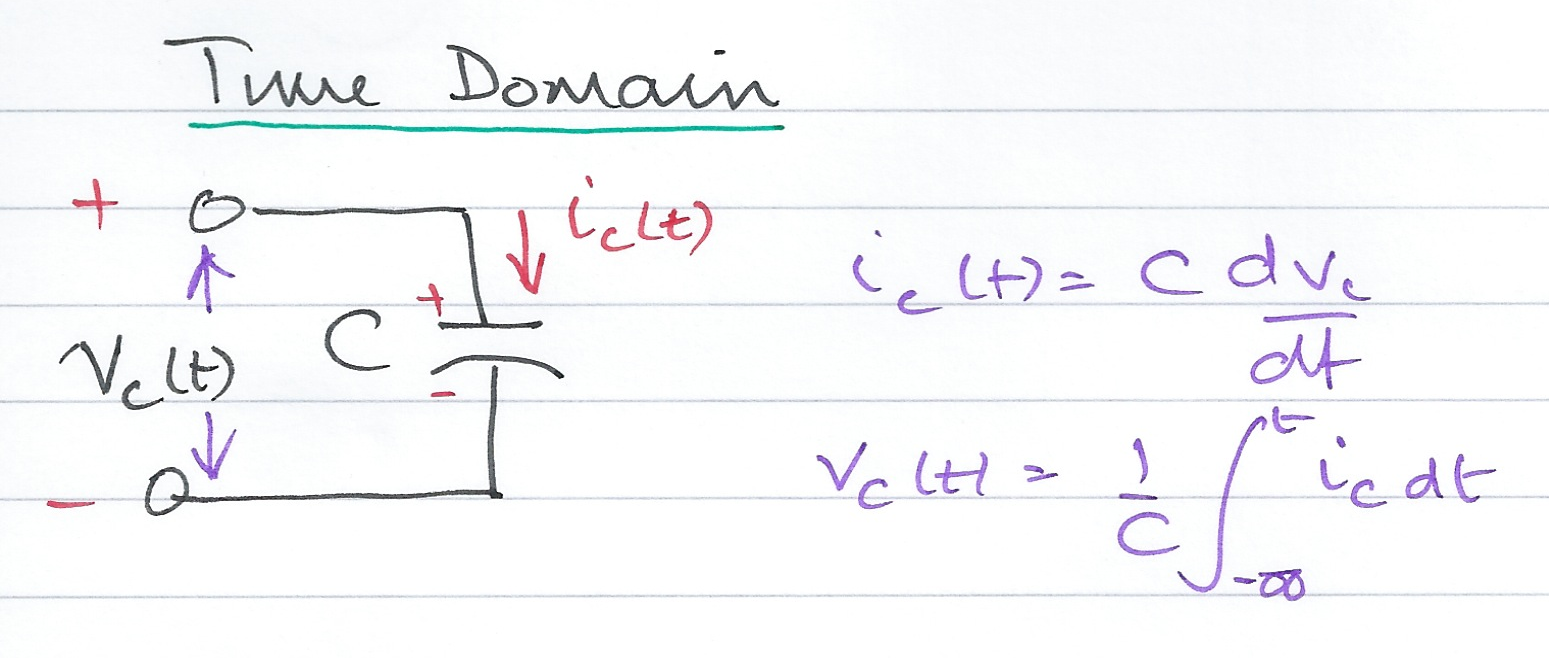
The current flowing into the capacitor is proportional to the change in voltage across the capacitor
(26)# \[i_C(t) = C \frac v_C(t) \]eqict = i_C(t) == C * diff(v_C(t))
eqict =
i_C(t) == C*diff(v_C(t), t)
The voltage across the capacitor is inversely proportional to the integral of the current flowing into the capacitor which is easily confirmed by taking the integral of both sides of (26) and rewriting the equation to isolate \(v_C(t)\)
int(lhs(eqict)) == int(rhs(eqict)); eqvct = isolate(ans,v_C(t))
eqvct =
v_C(t) == int(i_C(t), t)/C
Which can be rwritten nicely as
(27)# \[v_C(t) = \frac\int_<-\infty>^ i_C(t)\, dt\]From the previous results, which of the following equations represent the Laplace transform of the current flowing into, and the voltage across, the capacitor \(C\) ?
\[V_c(s)=sCI_C(s) - i_C(0^-)\] \[I_c(s) = sCV_C(s) - v_C(0^-)\] \[V_c(s) = \frac + \frac\] \[I_c(s)=\frac + \frac\]-> Open poll
We take the Laplace transforms of (26) and (27) to obtain
(28)# \[I_C(s) = s C V_C(s) - v_C(0^-)\] (29)# \[V_C(s) = \frac + \frac\]The current and voltage are transformed but so is the capacitance. The complex frequency representation has used the derivative property for the voltage across the capacitor and the integration property for the current flowing into the capacitor. The use of the dervative and integration transforms has introduced a term that depends on the initial voltage (initial charge) across the capacitor. Therefore, the initial voltage would need to be considered in computing the actual voltage and current introduced by the capacitor in the complex frequency domain.

Do exercises 12.1 and 12.2 Now
By analogy with the resistance of a resistor \(R\) , a component with complex impedance \(Z(s)\) satisfies Ohm’s law:
For the resistance \(R\) \(\Omega\) , inductance \(L\) H and capacitance \(C\) F, which of the following represent the complex impedance, \(Z(s) = V(s)/I(s)\) of the components?
-> Open Poll
Consider the \(s\) -domain RLC series circuit shown in Fig. 57 , where the initial conditions are assumed to be zero.
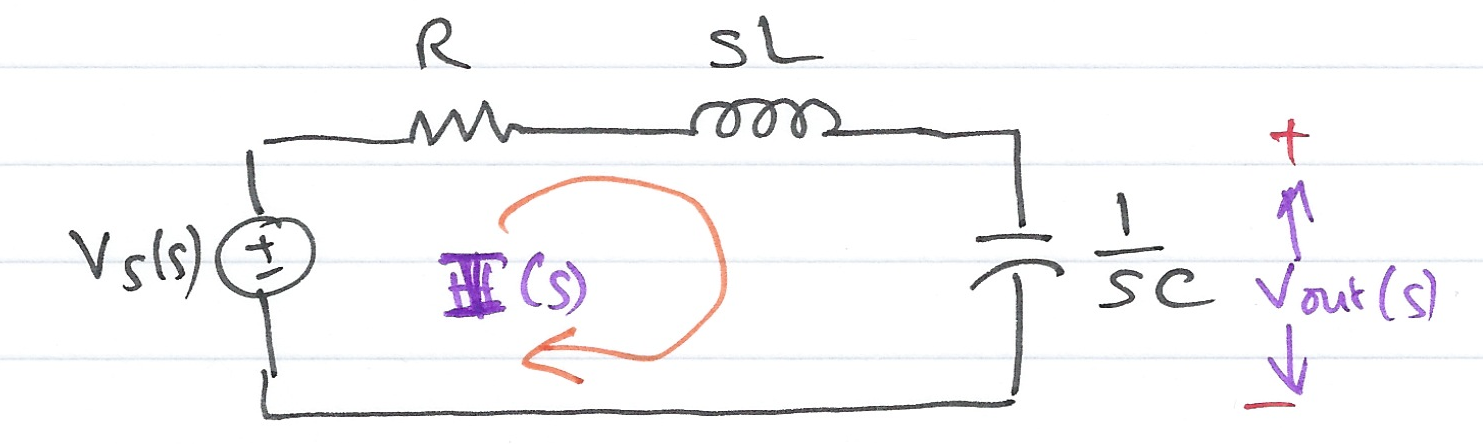
For this circuit, the sum
\[R + sL + \frac<1>\]represents that total opposition to current flow.
and defining the ratio \(V_s(s)/I(s)\) as \(Z(s)\) , we obtain
\[Z(s) = \frac = R + sL + \frac\]The \(s\) -domain current \(I(s)\) can be found from
\[Z(s) = R + sL + \frac<1>.\]Since \(s = \sigma + j\omega\) is a complex number, \(Z(s)\) is also complex and is known as the complex input impedance of this RLC series circuit.
By analogy with the admittance of a resistor \(G\) , a component with complex admittance \(Y(s)\) satisfies Ohm’s law:
For the resistance \(R\) \(\Omega\) , inductance \(L\) H and capacitance \(C\) F, which of the following represent the complex admittance, \(Y(s) = I(s)/V(s)\) of the components?
For the resistor \(R\) Ω, inductor \(L\) H and capacitance \(C\) F, which of the following represent the complex admittance of the components?
-> Open Poll
Consider the \(s\) -domain GLC parallel circuit shown in Fig. 58 where the initial conditions are zero.
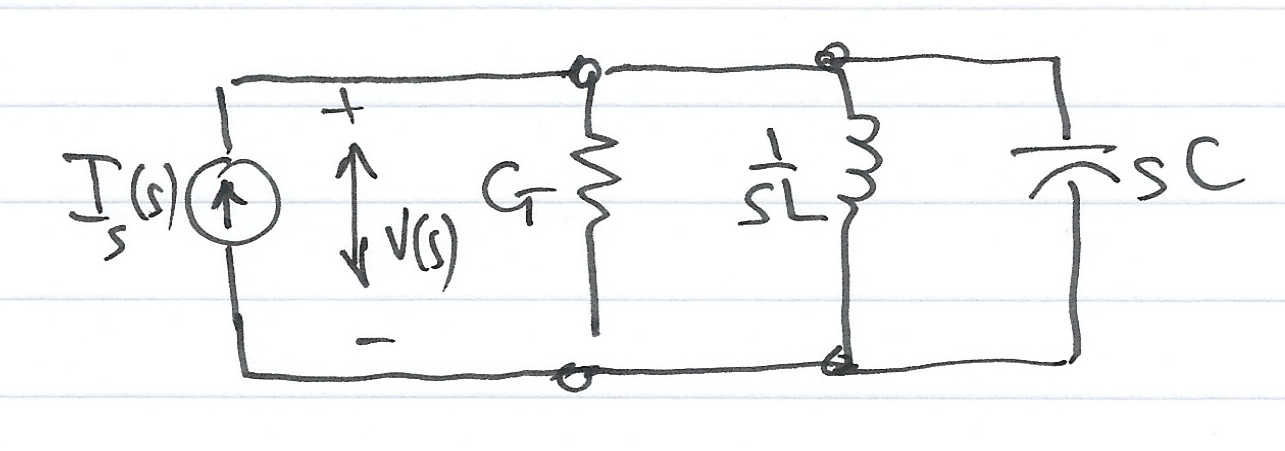
For this circuit
\[GV(s)+ \frac<1>V(s) + sCV(s) = I_s(s)\] \[\left(G+ \frac<1> + sC\right)V(s) = I_s(s)\]Defining the ratio \(I_s(s)/V(s)\) as \(Y(s)\) we obtain
\[Y(s)=\frac = G+ \frac + sC = \frac\]The \(s\) -domain voltage \(V(s)\) can be found from
\[Y(s) = G + \frac<1> + sC.\]\(Y(s)\) is complex and is known as the complex input admittance of this GLC parallel circuit.
We will work through these in class.
Use the Laplace transform method and apply Kirchoff’s Current Law (KCL) to find the voltage \(v_c(t)\) across the capacitor for the circuit in Fig. 59 given that \(v_c(0^-) = 6\) V.
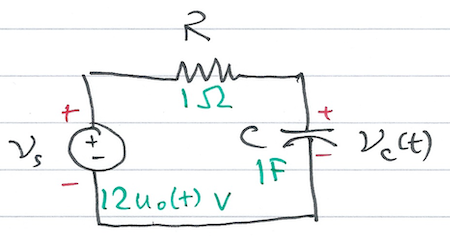
Use the Laplace transform method and apply Kirchoff’s Voltage Law (KVL) to find the voltage \(v_c(t)\) across the capacitor for the circuit shown in fig:12.2 given that \(v_c(0^-) = 6\) V.

We will solve this example by hand in Examples class 4 and then review the solution in MATLAB lab 5.
In the circuit shown in Fig. 61 , switch \(S_1\) closes at \(t=0\) , while at the same time, switch \(S_2\) opens. Use the Laplace transform method to find \(v_<\mathrm
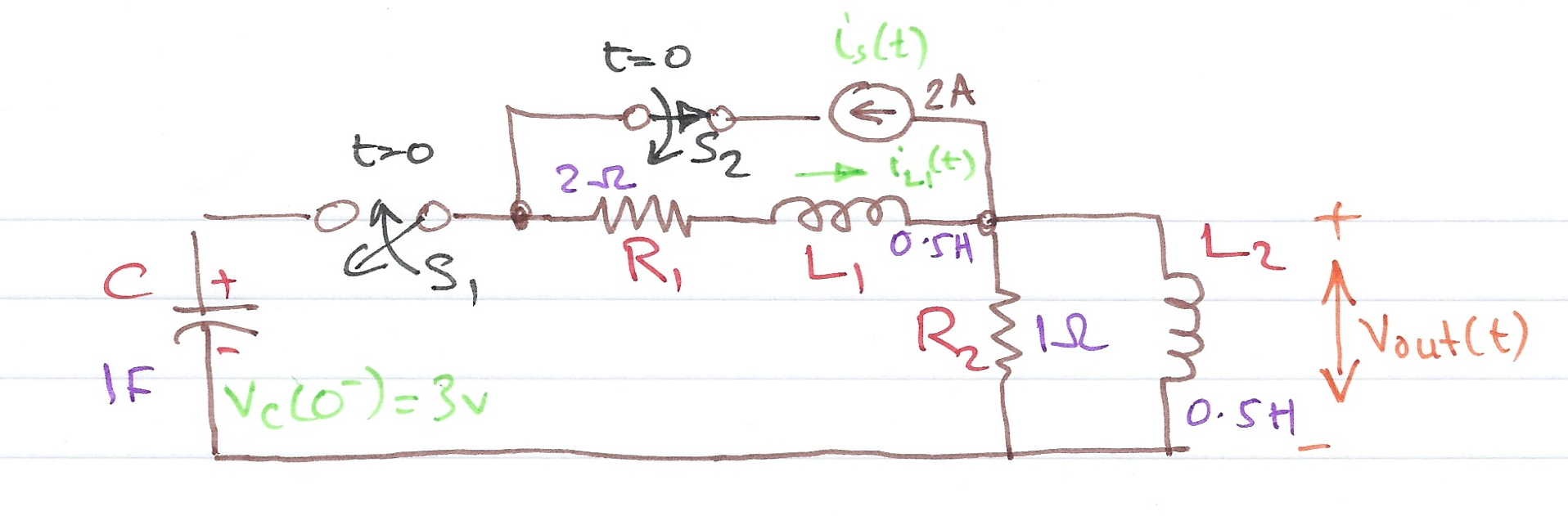
We can show how with the assistance of MATLAB (See solution12_3.mlx) that the solution is
(30)# \[V_<\mathrmand we can plot the result (see 4. Complete solution in MATLAB )
File Pencast: example12_3.pdf - Download and open in Adobe Acrobat Reader.
The attached PDF gives the solution to Exercise 12.3: A complex RLC circuit with initial conditions by hand. It’s quite a complex, error-prone (as you can see by the crosssings out!) calculation that needs careful attention to detail. This in itself gives justification to my belief that you should use computers wherever possible.
We will use a combination of pen-and-paper and MATLAB to solve this.
Draw equivalent circuit at \(t=0\)
Convert to transforms
Determine equation for \(V_(s)\) .
In the lecture we showed that after simplification for Exercise 12.3: A complex RLC circuit with initial conditions
We will use MATLAB to factorize the denominator \(D(s)\) of the equation into a linear and a quadratic factor.
p = roots([1, 8, 10, 4])
syms s t y = expand((s - p(2))*(s - p(3)))
y = sym2poly(y)
t=0:0.01:10; Vout = 1.36.*exp(-6.57.*t). +0.64.*exp(-0.715.*t).*cos(0.316.*t). -1.84.*exp(-0.715.*t).*sin(0.316.*t); plot(t, Vout); grid title('Plot of Vout(t) for the circuit of Example 3') ylabel('Vout(t) V'),xlabel('Time t s')
Vout = tf(2*conv([1, 0],[1, 3]),[1, 8, 10, 4])
impulse(Vout)
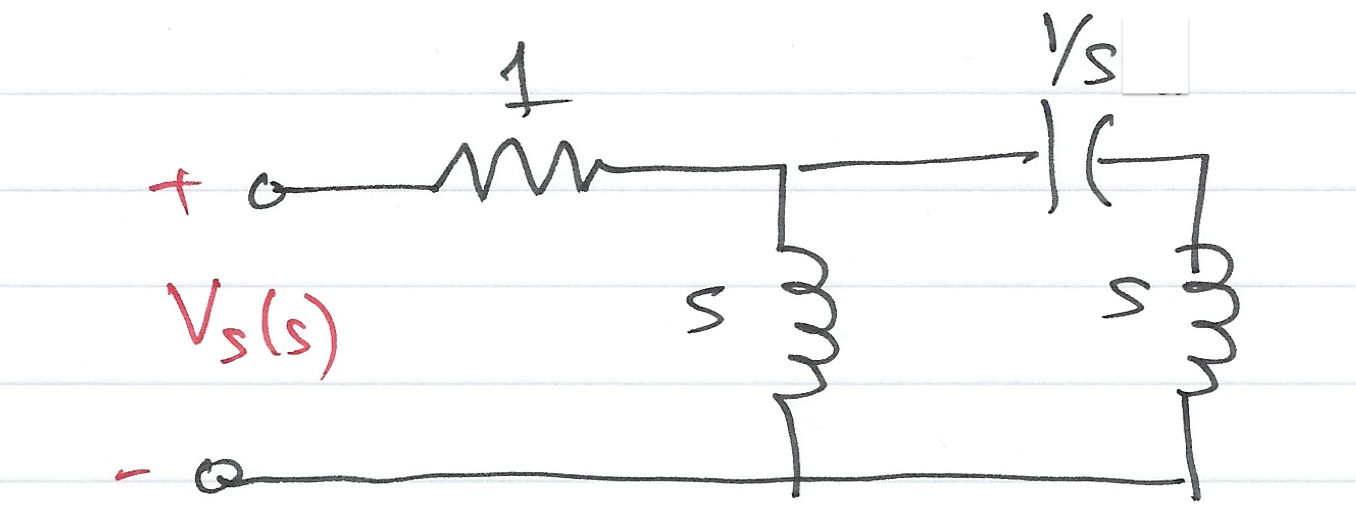
Consider Fig. 57 and give an expression for \(V_c(s)\) .
We will solve this examples by hand and then review the solution in MATLAB lab 5.
For the network shown in Fig. 62 , all the complex impedance values are given in \(\Omega\) (ohms).
Solutions: Pencasts ex4_1.pdf and ex4_2.pdf – open in Adobe Acrobat.
We will solve this examples by hand and then review the solution in MATLAB Lab 5.3.
Compute \(Z(s)\) and \(Y(s)\) for the circuit shown in Fig. 63 . All impedence values are in \(\Omega\) (ohms). Verify your answers with MATLAB.
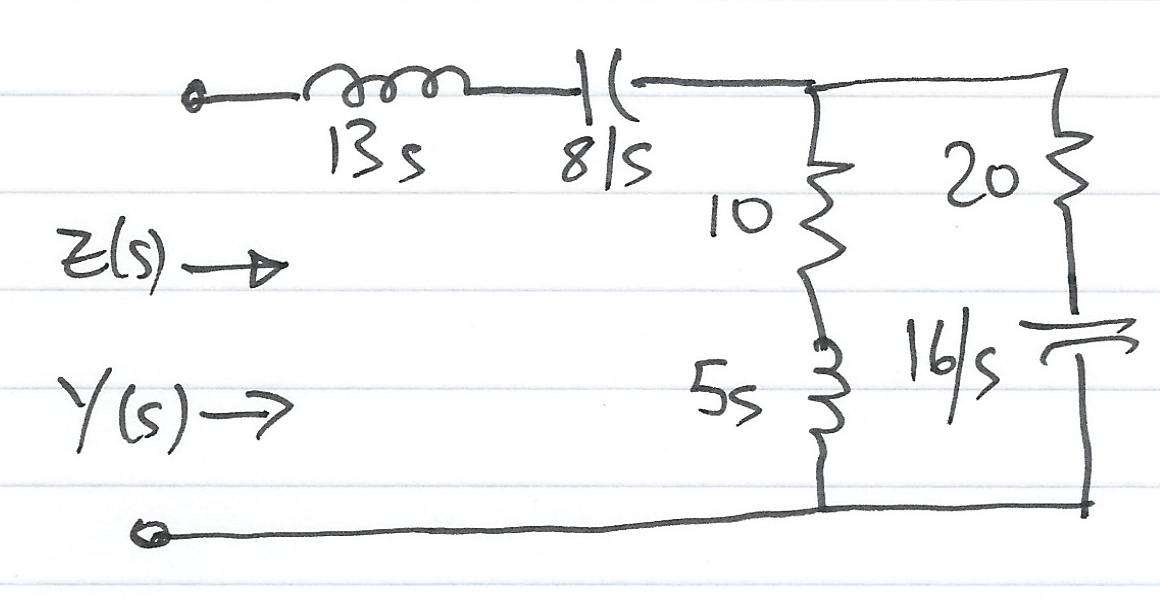
syms s; z1 = 13*s + 8/s; z2 = 5*s + 10; z3 = 20 + 16/s;
z = z1 + z2 * z3 /(z2 + z3)
z10 = simplify(z)
pretty(z10)
y10 = 1/z10; pretty(y10)
This is Exercise 4 from 4.7 Exercises from [Karris, 2012]
This example will be solved in MATLAB Lab 5.3.
For the s-domain circuit shown in Fig. 64
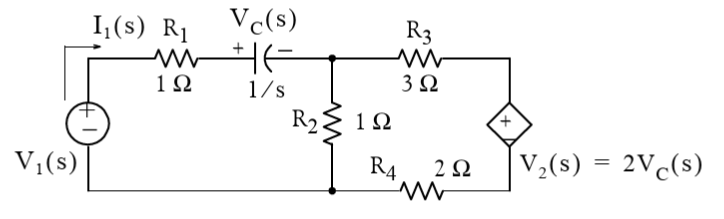
In MATLAB Lab 5, we will explore the tools provided by MATLAB for solving circuit analysis problems.
Complete any exercises that were not covered in the class or follow-up examples class. There are a number of related problems in Solved Problems 3.39—3.41 in [Hsu, 2020] and in section 4.7 Exercises in [Karris, 2012] .
Supplementary problems 3.52 and following ( [Hsu, 2020] ) provide opportunities for extra practice.
In this section we have looked at the application of the Laplace transform to circuit analysis.
Circuit analysis can be performed using Laplace transforms by using the Laplace transform equivalents of the component impedence or admittance. In particular, for impedence, we use \(R\) , \(sL\) and \(1/sC\) ; for admittance we use \(G = 1/R\) , \(1/sL\) , \(sC\) . Once the circuit has been reduced to a rational polynomial in \(s\) , the inverse laplace transform can be used to determine the time response of the circuit.
When dealing with components using their complex component equivalents, the usual circuit analysis rules, KVL, KCL, voltage-divider rule, etc, can all be used.
The complex impedence of a circuit is the resistance to current flow and is given by the general law \(V(s) = Z(s) I(s)\) from which the impendence is given by \(Z(s) = V(s)/I(s)\) . Similarly, the complex admittance of a circuit is given by \(Y(s) = I(s)/V(s)\) .
The complex admittance is the reciprocal of the complex impedence \(Y(s) = 1/Z(s)\) .
Though not a consequence of the Laplace transform, it is worth noting that the use of impedence facilitates the analysis of circuits for which the components are commected in series; for circuits with parallel connection of components, the use of admittance facilitates the analsysis.
We move on to consider
Hwei P. Hsu. Schaums outlines signals and systems. McGraw-Hill, New York, NY, 2020. ISBN 9780071634724. Available as an eBook. URL: https://www.accessengineeringlibrary.com/content/book/9781260454246.
Steven T. Karris. Signals and systems with MATLAB computing and Simulink modeling. Orchard Publishing, Fremont, CA., 2012. ISBN 9781934404232. Library call number: TK5102.9 K37 2012. URL: https://ebookcentral.proquest.com/lib/swansea-ebooks/reader.action?docID=3384197.
For convenience, single script MATLAB solutions to the examples are provided and can be downloaded from the accompanying MATLAB folder in the GitHub repository.
Unit 4.4 The Inverse Laplace Transform
Unit 4.6: Transfer Functions